Introduction to Prime Numbers

I. What is a Prime Number?

A number is called prime if it satisfies all the following conditions:

is a natural number,
greater than 1,
has only 2 divisors: 1 and itself.

For example, $\{ 2, 3, 5, 7 ,11, 13, 17, 19 \}$ are the first prime numbers.

If so, what is NOT a prime number?

not a natural number (e.g. a fraction, like $\frac{1}{2}$ or $\frac{14}{5}$ ),
less than or equal to 1 (e.g. -3, 0, 1 are NOT prime),
can be formed by multiplying 2 natural numbers less than itself (e.g. 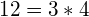$12 = 3 * 4$ is NOT a prime number).

II. Why is Prime Number important?

In the modern world, prime numbers are crucial for:

Hashing
Cryptography

1. Hashing

In competitive programming, Hashing is a great technique, which is often used when dealing with complex string operations.

Usually, each sub-string is hashed to a number (we represent each sub-string by a number). 2 equal sub-strings will always be transformed to the same number. 2 different sub-strings will most likely be transformed into 2 different numbers. The case when 2 different sub-strings are transformed to the same number is called Collision. When doing hash, we want to make collisions as less likely to happen as possible.

The concept of prime numbers is the key to reduce the chance of collision.

To be more precise, when the distribution of your “keys” (your sub-strings as in the above example) is not uniform, many of your keys are in the form: y = ka + b with constant b, and somehow a is a divisor of MOD, then there will be many collisions. Hence, to be careful, we can set a prime number for MOD, and because prime numbers do not have any divisors other than 1 and itself, the bad case described above will not happen.

If you are a bit confused about Hashing, MOD or any terms from this Hashing section, please take a look at Introduction to Hashing.

2. Cryptography

Modern cryptography uses prime numbers a lot. Private-public key algorithms exploit the fact that: it is easy to multiply 2 prime numbers, but very very hard to factorize a big number back to primes. You can imagine that a big number is a number that has 100 (or more) digits in its decimal representation.

RSA and Digital Signature are the most famous examples.

III. How to test for primality?

Given a number x, we need to determine if x is a prime number or not.

1. Exhaustive search

Straightforward from the definition of a prime number, we can determine whether x is prime by looping through every number in the range $[2, x-1]$ , x is prime if and only if none of these numbers divides x.

bool isPrime(int x) {
     
    if (x < 2)
        return false;
     
    for (int i = 2; i < x; ++i)
        if (x % i == 0)
            return false;
     
    return true;
     
}

Complexity: $O(n)$

2. Exhaustive search (enhanced)

We can reduce the complexity of the above algorithm by an observation: if $x \geq 2$ and x is NOT a prime number, then we can write $x = a*b$ with $a \geq 2$ , $b \geq 2$ and $min(a, b) \leq \sqrt{x}$ .

Why? Because if both $a > \sqrt{x}$ and $b > \sqrt{x}$ are true, then $a*b > \sqrt{x} * \sqrt{x} = x$ . Contradict with the fact that $a*b = x$ .

bool isPrime(int x) {
     
    if (x < 2)
        return false;
     
    int sqrtx = sqrt(x);
     
    for (int i = 2; i <= sqrtx; ++i)
        if (x % i == 0)
            return false;
     
    return true;
     
}

Complexity: $O(\sqrt{n})$

3. Miller-Rabin test

Miller-Robin primality test is a probabilistic test, that is, the test USUALLY outputs the right result (NOT ALWAYS). To be a little bit more specific, when the test outputs False (the test says that x is not a prime number), it is absolutely true that x is not prime number, but when the test outputs True, we know that x is likely to be a prime number (but we are not 100% sure).

Good news is that we have a way to make this test deterministic for 32-bit and 64-bit integer numbers. Because the explanation is a bit complex and lengthy, I will move it to a separated post. Follow this link to see it!

Complexity: $O(k*(\log{n})^{3})$ or better (with k ~ 12 for 64-bit integer)

4. Test for primality in $O(1)$ with pre-processing (using Sieve of Eratosthenes)

Sieve of Eratosthenes is a technique to pre-compute all prime numbers in the range (1, n]. It also supports testing for the primality of any number in the above range in $O(1)$ time complexity.

Complexity:

pre-processing: $O(n*\log{\log{n}})$ and can be enhanced to $O(n)$
test for primality: $O(1)$

Details about this technique can be found Here

IV. Practice Problems

SPOJ – PON

V. Further Reading

Sieve of Eratosthenes

Prime factorization

Totient function

RSA

Digital Signature

Tung M Phung's Blog

Introduction to Prime Numbers

Leave a ReplyCancel reply