Regularization for Linear regression

Test your knowledge

In this blog post, we will go through every aspect of Regularization for Linear regression models by answering the following 5 questions:

What is Regularization?
When to use Regularization?
Where to use Regularization?
How to use Regularization?
Why does Regularization work?

a bonus,
Other regularization techniques

and lastly,
Conclusion.

What is Regularization?

Literally, Regularization means making something more regular. It is somehow true even in the sense of Machine learning.

In Machine learning, Regularization is a process of making your predictive model more “regular” – that is, more natural, more simple, more “real“.

For example, making all the weights ( $w_i$ for $\forall i$ ) more equal to each other. This is analogous to making a shape more regular by tweaking so that all the edges have the same length, right?

When to use Regularization?

Regularization is a technique used to combat the problem of over-fitting, so we are using it in case our model seems to over-fit the data.

Where to use Regularization?

We use Regularization in the objective function (or we can say the cost function).

How to use Regularization?

To apply Regularization, we just need to modify the cost function, by adding a regularization function at the end of it.

New cost function = Original cost function + regularization function.

Then, we optimize the New cost function instead of the Original cost function.

There are several Regularization methods for Linear regression. We are going to examine each of them:

Lasso (also called L1)

New cost function = Original cost function + $\lambda \sum_{1 \leq i \leq n}|w_i|$ ,

where:

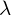$\lambda$ is the rate of Regularization. This parameter controls if regularization’s influence on your model is high or low. Higher 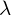$\lambda$ means higher the influence of regularization. $\lambda > 0$ .
$\lambda \sum_{1 \leq i \leq n}|w_i|$ is the Lasso regularization function.

For example, if you originally use MAE as your cost function, then after applying Lasso, your new cost function will be:

New cost function = $\frac{1}{n} \sum_{1 \leq i \leq n}|y_i - y_i'| + \lambda \sum_{1 \leq i \leq n}|w_i|$ .

Ridge (also called L2)

New cost function = Original cost function + $\lambda \sum_{1 \leq i \leq n}(w_i)^2$ ,

Interpretation of the parameters is very similar to above:

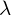$\lambda$ is the rate of Regularization. This parameter controls if regularization’s influence on your model is high or low. Higher 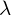$\lambda$ means higher the influence of regularization. $\lambda > 0$ .
$\lambda \sum_{1 \leq i \leq n}(w_i)^2$ is the Ridge regularization function.

For example, if you originally use MSE as your cost function, then after applying Ridge, your new cost function will be:

New cost function = $\frac{1}{n} \sum_{1 \leq i \leq n}(y_i - y_i')^2 + \lambda \sum_{1 \leq i \leq n}(w_i)^2$ .

Note that the value of $\lambda$ is your choice. When you feel that your model is still over-fitting, increase $\lambda$ . On the other hand, if you think your model escaped from over-fitting but is now under-fitting, just decrease $\lambda$ .

Elastic Net

New cost function = Original cost function + $\lambda_1 \sum_{1 \leq i \leq n}|w_i|+ \lambda_2 \sum_{1 \leq i \leq n}(w_i)^2$ ,

where:

$\lambda_1$ is regularization rate of Lasso,
$\lambda_2$ is regularization rate of Ridge.

Elastic Net Regularization is simply a combination of Lasso and Ridge. You can customize the effect of Lasso and Ridge separately using $\lambda_1$ and $\lambda_2$ .

Why does Regularization work?

What Regularization actually does is to reduce the magnitude of the weights ( $w_i$ , with $\forall i$ ) while keeping the original cost small enough. Hence, we shift our question to Why reducing the weights helps with the problem of over-fitting?

To answer this question, we can look at it from either of the below 2 viewpoints:

Viewpoint 1: over-fitting is that you emphasize on the wrong predictors. And the only way for you to emphasize a predictor is putting more weight on it. Hence, by reducing the weights, you also reduce your emphasis, or says, reduce your over-fitting.

Viewpoint 2: Look at this picture of over-fitting:

I bet you already saw some similar pictures like this (but probably more beautiful ones) if you have ever tried to find out some information about over-fitting. But if you haven’t, let me introduce: the red points are response values of data, while the blue line is the regression model. We clearly see that the line (the model) is over-fitting the data.

Notice that the slope of the line changes fiercely to match the data points. A line can have its slope changing like that if and only if the magnitudes of parameters (the weights) are large and have high variance. Hence, by reducing the magnitudes of the weights, we flatten the line and help it less over-fit the data.

Other regularization techniques

Some other techniques for preventing over-fitting are:

Collecting more data and/or data augmentation (e.g. in Computer Vision, in most cases, we can rotate the existing images).
Noise addition. This approach is a bit unintuitive at first glance: we intentionally add some noise to our data. This works because it forces our models to concentrate on the true underlying patterns of the data instead of small, random noise.
Early stopping. If our process to make the regressor is iterative (e.g. Gradient Descent), we can set an upper limit for the number of iterations it can do, so that the models can stop right before they attempt to model the noise.

Test your understanding

Conclusion

Above, we learned about the 5 aspects of Regularization.

Essentially, Regularization is a technique to deal with over-fitting by reducing the weights of linear regression models.

Lasso tries to decrease the absolute value of the weights. Hence, some features with little or no effect on the model will get eliminated (i.e. weight equals 0).

Ridge, on the other hand, decreases the squared value of the weight. Hence, features with larger weights will be punished more heavily than features with smaller weights. In the end, usually, there are no features that have weights equal to 0. Instead, bad features will still have weight, although very very small. The weights after applying Ridge will be like the edges of regular shape (i.e. having comparable values) if the features’ influence on the model is quite comparable to each other.

Elastic net, as the combination of Lasso and Ridge, is in the middle of the 2. Elastic Net will be more like Lasso or more like Ridge depends on the values of $\lambda_1$ and $\lambda_2$ .

Regularization, especially Lasso, can also help in feature selection.

Beside L1, L2 and Elastic Net, some other techniques for fighting over-fitting are: collecting more data, noise addition, and early stopping.

An important note: remember to scale all the features (the predictors) before applying Linear regression with Regularization (L1, L2, ElasticNet), because this will make the Regularization Function treat the predictors equally.

You can find the full series of blogs on Linear regression here.

Tung M Phung's Blog

Regularization for Linear regression

Leave a ReplyCancel reply