
| Test your knowledge |
| |
Naive Bayes is a very popular algorithm in Machine Learning given its simplicity, rigid performance and interesting idea from Bayesian Probability.
In this blog post, we show and explain the Bayes formula, how to build a Naive Bayes classifier (with your pen and paper or with Python-sklearn), the assumptions behind this method together with its strengths and weaknesses.
The curriculum is as below:
Table of content
Naive Bayes method
Example
Laplace smoothing
Naive Bayes with Python
Assumptions
Strengths
Weakness
Naive Bayes method
Naive Bayes classifier algorithm relies on Bayes’ theorem about the probability of an event given prior knowledge related to it. The theorem is simply:
![]()
where:
- A and B are 2 events.
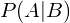 is the conditional probability of A given B is true.
is the conditional probability of A given B is true. is the conditional probability of B given A is true.
is the conditional probability of B given A is true. and
and  are the probabilities of A and B, respectively.
are the probabilities of A and B, respectively.
This formula is true because ![]()
(where ![]() denotes the joint probability of both events A and B – the probability that both A and B are true).
denotes the joint probability of both events A and B – the probability that both A and B are true).
In the context of Machine Learning and Classification, we can rewrite the formula as below:
![]()
where:
 is the i-th class.
is the i-th class. 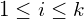 with k is the number of classes.
with k is the number of classes.- X is the training data. Note that X represents 1 sample data point (not the entire dataset).
 is the probability that the sample data point X belongs to class i.
is the probability that the sample data point X belongs to class i. is the probability of the data point X to appear in class i.
is the probability of the data point X to appear in class i.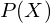 is the probability of X.
is the probability of X.
To find the most suitable class for each data point X, we find all the ![]() for
for ![]() , and then we assign X to the class with the highest probability.
, and then we assign X to the class with the highest probability.
In other words, we find arg max ![]() of
of ![]() .
.
Or say, arg max ![]() of
of ![]()
Notice that the value of ![]() is constant across all classes. So, we can safely ignore it and adjust our goal to finding arg max
is constant across all classes. So, we can safely ignore it and adjust our goal to finding arg max ![]() of
of ![]() .
.
![]()
![]() is easily computed by taking the proportion of class i in our whole dataset.
is easily computed by taking the proportion of class i in our whole dataset.
![]() , where n is the sample size and
, where n is the sample size and ![]() is the number of data samples that belong to class i.
is the number of data samples that belong to class i.
![]()
![]() requires a bit more work. Be reminded that X is a vector of values,
requires a bit more work. Be reminded that X is a vector of values, ![]() (
(![]() , where m is the number of predictor variables) is the value of the predictor variable j for this data point X.
, where m is the number of predictor variables) is the value of the predictor variable j for this data point X.
We make an assumption here that the predictor variables are all independent of each other.
Thus, ![]() .
.
If the j-th predictor variable is a categorical variable, ![]() can be simply calculated from the training dataset. In case it is a numerical variable, we may either distribute the values into bins and then each bin is treated as a categorical value, or assume its distribution (e.g. Gaussian distribution) and then take the PDF.
can be simply calculated from the training dataset. In case it is a numerical variable, we may either distribute the values into bins and then each bin is treated as a categorical value, or assume its distribution (e.g. Gaussian distribution) and then take the PDF.
Example
Suppose our task is to classify the type of animal given its fur color and the sharpness of its claws. The training data looks like below:
Naive Bayes example training data
| No. | Fur color | Sharpness of claws | Animal |
|---|---|---|---|
| 1 | Black | High | Cat |
| 2 | Yellow | Low | Cat |
| 3 | Black | High | Cat |
| 4 | Blue | High | Cat |
| 5 | Yellow | Low | Dog |
| 6 | Blue | Low | Dog |
| 7 | Yellow | High | Dog |
| 8 | Black | Low | Dog |
and here is the testing data:
Naive Bayes example testing data
| No. | Fur color | Sharpness of claws | Animal |
|---|---|---|---|
| 9 | Yellow | Low | ? |
| 10 | Black | High | ? |
We now pre-compute some values with the information provided by the training data. These values are then used to predict the samples in the testing set.
First, we need the probability of each class.
P(Cat) = ![]() = 0.5
= 0.5
P(Dog) = ![]() = 0.5
= 0.5
Then, we compute the conditional probability of each category given a class.
P(Fur = Black | Cat) = ![]()
P(Fur = Black | Dog) = ![]()
P(Fur = Yellow | Cat) = ![]()
P(Fur = Yellow | Dog) = ![]()
etc.
Until we have all the conditional probabilities P(category | class) as in the below table.
Naive Bayes example P(category | class)
| Class | Fur | Sharpness | |||
|---|---|---|---|---|---|
| Black | Yellow | Blue | High | Low | |
| Cat | 0.5 | 0.25 | 0.25 | 0.75 | 0.25 |
| Dog | 0.25 | 0.5 | 0.25 | 0.25 | 0.75 |
We have done the training part. Now, it’s time for predictions. We will predict the classes of 2 testing examples shown above.
For the first testing sample (the sample with index No. 9):
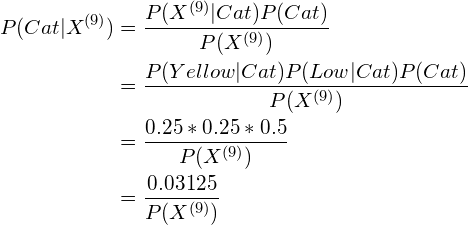
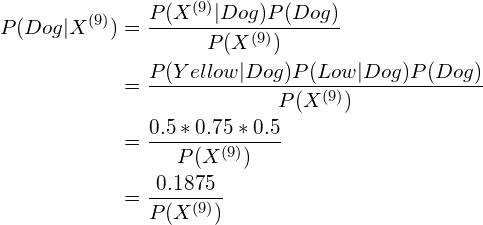
As we know ![]() is a positive number (because
is a positive number (because ![]() is the probability of
is the probability of ![]() , and the probability of an already-happened-event is always larger than 0), we have
, and the probability of an already-happened-event is always larger than 0), we have ![]() .
.
Thus, according to the Naive Bayes algorithm, sample No. 9 is classified as Dog.
For the second testing sample (the sample with index No. 10):


Hence, we conclude the sample No.10 is classified as Cat.
Laplace Smoothing
In practice, for categorical variables, it sometimes happens that a category in the testing set does not appear in the training set (e.g. in the above example, what if, in sample No.9, the fur color is Pink instead of Yellow?). In these cases, the results we output are all 0, which gives no clue about which class we should assign the data point to.
To resolve this issue, we often apply Laplace smoothing to the computation of the probabilities.
In other words, instead of the conventional formula:
![]()
we use the Laplace estimate:
![]()
where:
 is the value of the sample at the i-th feature.
is the value of the sample at the i-th feature. is the j-th categorical value of feature i.
is the j-th categorical value of feature i. is the k-th class.
is the k-th class. is the number of samples in
is the number of samples in  that has
that has 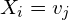 .
. is the number of samples of class k.
is the number of samples of class k. is the number of possible values for
is the number of possible values for  .
.
For example, if we apply to the problem above:
P(Fur = Black | Cat) = ![]()
Naive Bayes with Python
To run the Naive Bayes algorithm in Python, we could use the pre-built functions from sklearn library, which can be found in sklearn.naive_bayes:
Assumptions
Strengths
Weaknesses
| Test your understanding |
| |
References: