
Exponential Linear Unit (ELU), proposed by Djork-Arné in 2015, is a variant of the so-called ReLU nonlinearity. Through various experiments, ELU is accepted by many researchers as a good successor of the original version (ReLU).
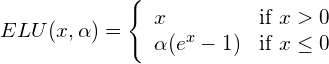

 . Note that the value
. Note that the value 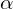 is pre-defined by the user, i.e. it is not learned by the network.
is pre-defined by the user, i.e. it is not learned by the network.While ELU’s output may not be smaller than or equal to –![]() , the upper bound is clearly undefined (it goes to infinity). Hence, ELU is a non-saturated nonlinearity.
, the upper bound is clearly undefined (it goes to infinity). Hence, ELU is a non-saturated nonlinearity.
In practice, ![]() is often set to be 1.0 or in the range [0.1, 0.3].
is often set to be 1.0 or in the range [0.1, 0.3].
The derivative of ELU is given by:

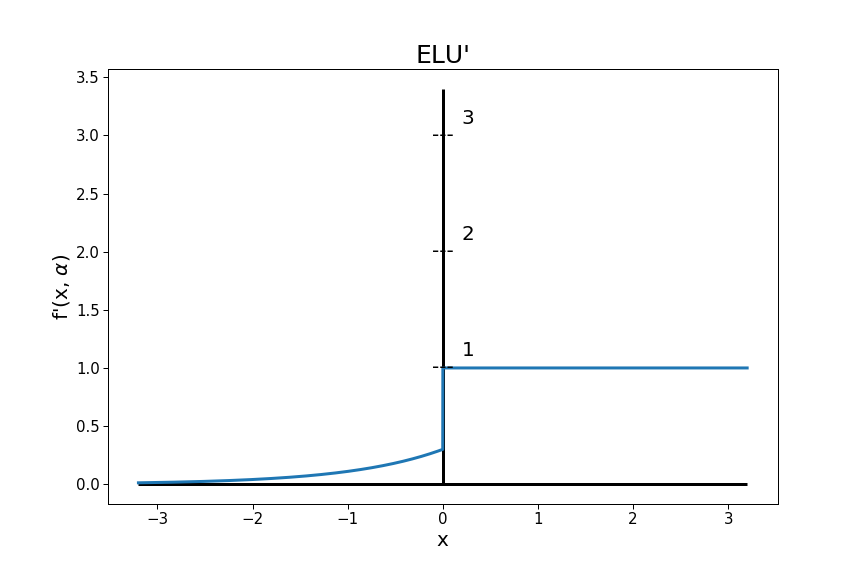
Advantages
![]() The dying ReLU problem no longer exists, as both negative and positive inputs are transformed to non-0 outputs.
The dying ReLU problem no longer exists, as both negative and positive inputs are transformed to non-0 outputs.
![]() Outputs can be either positive or negative. Studies showed that functions with 0-centered outputs help networks train faster. Although ELU’s outputs are not distributed around 0, the fact that it does produce negative values makes it be preferred in this sense compared to ReLU. In practice, it seems that networks with ELU converge more quickly than with ReLU, even though the exponential computation in ELU (
Outputs can be either positive or negative. Studies showed that functions with 0-centered outputs help networks train faster. Although ELU’s outputs are not distributed around 0, the fact that it does produce negative values makes it be preferred in this sense compared to ReLU. In practice, it seems that networks with ELU converge more quickly than with ReLU, even though the exponential computation in ELU (![]() ) requires longer processing time.
) requires longer processing time.
![]() ELU is not piece-wise linear, this makes it model the non-linearity better.
ELU is not piece-wise linear, this makes it model the non-linearity better.
![]() The plateau in the negative region helps in maintaining robustness and stability.
The plateau in the negative region helps in maintaining robustness and stability.
Disadvantages
![]()
![]() is fixed, not learned.
is fixed, not learned.
![]() It still suffers from Gradient Exploding and Gradient Vanishing Problem, thus the help of normalization methods may remain necessary sometimes (e.g. this paper). SELU, which was built from ELU with an innate ability to self-normalize, was introduced to address this problem.
It still suffers from Gradient Exploding and Gradient Vanishing Problem, thus the help of normalization methods may remain necessary sometimes (e.g. this paper). SELU, which was built from ELU with an innate ability to self-normalize, was introduced to address this problem.
![]() It is not 0-centered. Although ELU does produce negative outputs, the fact that it is not 0-centered makes it seemingly sub-optimal. Another nonlinearity called Parametric ELU is introduced to mitigate this issue.
It is not 0-centered. Although ELU does produce negative outputs, the fact that it is not 0-centered makes it seemingly sub-optimal. Another nonlinearity called Parametric ELU is introduced to mitigate this issue.
![]() No sparsity. ReLU outputs 0 for negative inputs, which is bad in some senses but also good in some others, as elaborated in this post.
No sparsity. ReLU outputs 0 for negative inputs, which is bad in some senses but also good in some others, as elaborated in this post.
| Test your understanding |
|
|
Performance Comparison
Experiment from ELU’s authors
Experiment 1:
Objective: To compare the performance of ELU with ReLU and Leaky ReLU on a simple classification task.
Experimental Design:
Result:

Verdict: While ReLU and Leaky ReLU had similar behaviors after 10 epochs of training with the loss around 0.15, ELU expressed a stronger power that nearly converged after 5 epochs with only 0.1 cross-entropy loss.
Experiment 2:
Objective: To compare the performance of ELU versus ReLU and Leaky ReLU on unsupervised learning.
Experimental Design:
Result:

Verdict: This result implies the superiority of ELU over the other 2 activations while its error rates are clearly the lowest for every choice of learning rate.
Experiment 3:
Objective: To compare the performance of ELU versus ReLU, Leaky ReLU and SReLU on a more complex supervised learning task.
Experimental Design:
(More details about the configuration can be found in the paper here.)
Result:
Without BatchNorm:
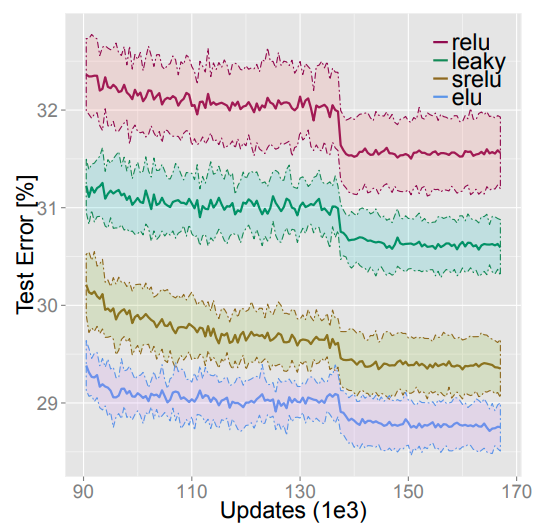
With BatchNorm:



Verdict: It is shown that ELU outperforms the remaining activations, even when they are helped by BatchNorm. Furthermore, there is some evidence that adding BatchNorm does not enhance a network with ELU but may even make its error rate higher.
Experiment 4:
Objective: To compare the performance of a CNN network with ELU versus other renowned CNN architectures.
Experimental Design:
(More details about the configuration can be found in the paper here.)
Result:

Verdict: It is shown that the network with ELU gave the lowest error rate for CIFAR-100. Furthermore, it is also ranked second on CIFAR-10.
Experiment 5:
Objective: To compare ELU and ReLU on the ImageNet dataset.
Experimental Design:
Result:
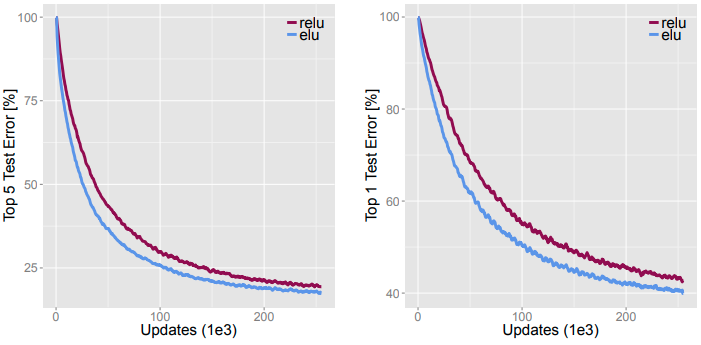
Verdict: This result shows that the network with ELU reduces the error rate faster than with ReLU in terms of the number of iterations. To reach a 20% Top-5 error rate, ELU needs only 160k iterations, this number is 200k iterations for ReLU.
Note that the speed of using ELU is slower by 5% compared with using ReLU.
Experiments from others
Experiment 1:
Source: Deep Residual Networks with Exponential Linear Unit
Objective: To compare the performance of the original ResNet (which uses a combination of ReLU + BatchNorm) and the same network but changed to use ELU instead.
Experimental design:

Result:
The 2 architectures are trained with different depths.

Verdict: The new ResNet with ELU gives higher performance regardless of the depth.
Experiment 2:
Source: Deep Residual Networks with Exponential Linear Unit
Objective: To compare the new network architecture (the modified ResNet using ELU) with other state-of-the-art methods.
Experimental design:
Result:

Verdict: The modified ResNet with ELU shows the best performance.
Experiment 3:
Source: On the Impact of the Activation Function on Deep Neural Networks Training
Objective: The original purpose of this experiment is to highlight the effectiveness of Edge of Chaos (EOC), which is a specific choice of hyperparameters as described in Schoenholz, 2017. However, we can adapt the result to compare the time to convergence of networks using ELU, ReLU and Tanh nonlinearities.
Experimental design:
(More details about the configuration can be found in the paper here.)
Result:
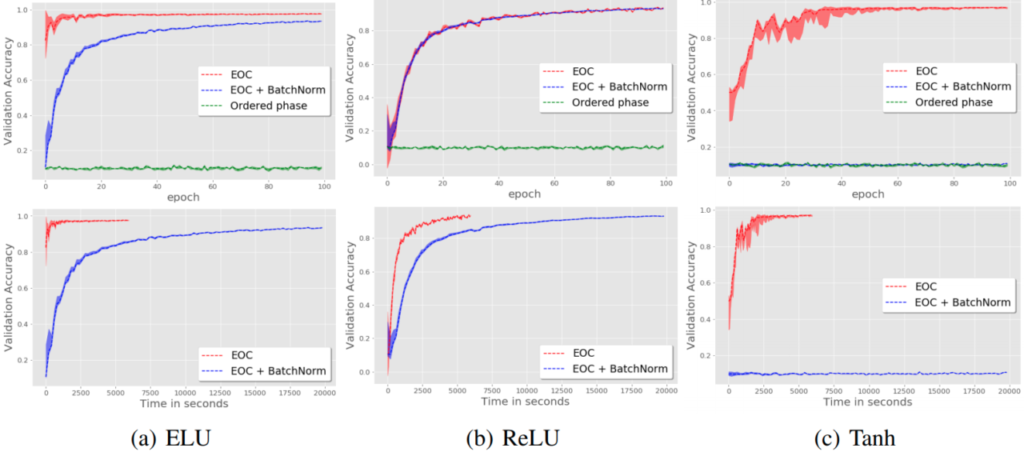
Verdict: In terms of speed, ELU outperforms ReLU and Tanh in this experiment, given that it converges after sufficiently less time and epochs than the other 2 activations.
Experiment 4:
Source: sonamsingh19.github.io
Objective: To compare the performances of ReLU and ELU activation functions for long dependencies.
Experimental design:
Result:

Verdict: ELU reaches an accuracy of around 96% after 15 epochs while ReLU struggles below 85%.
Conclusion
In this article, we discussed the ELU activation function for Deep Learning. Compared to the canonical ReLU, ELU is a bit more involved in the computation, however, with its various advantages, in practice, networks using ELU is not significantly slower than using ReLU (in fact, some experiments indicate that using ELU may even boost the speed for a large amount). Furthermore, there is evidence that ELU outperforms many other activations in terms of accuracy and error rate. Henceforth, many researchers have assumed using ELU as an enhanced version to replacing ReLU as their default nonlinearity.
References:
- The original paper of ELU by Djork-Arné: link
- Deep Residual Networks with Exponential Linear Unit by Shah et al.: link
- On the Impact of the Activation Function on Deep Neural Networks Training by Hayou et al.: link
- ML Low hanging Fruit: If you are using RNN for long dependencies: Try ELU: link
- A Simple Way to Initialize Recurrent Networks of Rectified Linear Units by Quoc et al.: link
- Deep Information Propagation by Schoenholz et al.: link