
Last time, we introduced Z-score and the Z-family. Today, we visit another house to meet the family of the T, consisting of T-statistic, T-test, T-distribution, etc.
Definition of the T-
The T-family is very similar to the Z-family, it acts as a substitution or approximation for the Z-family in some cases.
Depending on the input that we choose to use the Z- or the T-. We use T-family when:
- We don’t know the true variance of the distribution that the sample(s) is drawn from, or
- the sample size is
 30.
30.
otherwise, we use Z-family.
T-test
T-test refers to any hypothesis test that its result follows a T-distribution.
In practice, the tests are usually about the mean of 1 or 2 sample sets.
There are crucially 3 types of T-tests, those are:
One-sample T-test
‘One-sample‘ here does not mean a sample set of size 1, be careful, it is a bit confusing! In fact, this test is about one set of samples (with set size ![]() 2).
2).
Formally, One-sample T-test tests whether the mean of a sample set (![]() ) is significantly different from a population mean (
) is significantly different from a population mean (![]() ) or not.
) or not.
The hypothesis test’s structure is:

If you are familiar with Z-test, you will catch up with the T-test right away, because they are really close.
First, we compute the t-statistic (t):
![]()
with degree of freedom (d.f) = n-1.
The formula of t-statistic is comparable to that of z-statistic, with 2 differences:
- Use sample standard deviation (s) instead of population standard deviation (
 ). This is because we do not know the value of
). This is because we do not know the value of  , thus s is used as an approximation.
, thus s is used as an approximation. - There is a new term: the degree of freedom (explanation in Appendix A).
Example:
We have a set of 4 sample data points and their values are 20, 40, 55, 30. Hence, our sample mean is 36.25 and the standard deviation of ![]() 12.93. We want to test the hypothesis that this sample set is sampled from a population with the mean 40, the significance level (
12.93. We want to test the hypothesis that this sample set is sampled from a population with the mean 40, the significance level (![]() ) for this test is 0.1.
) for this test is 0.1.
We don’t know the population’s standard deviation, and even more, the sample size is not greater than 30, thus we use the T-test instead of the Z-test. In fact, both conditions for using the T-test are satisfied, while we need just 1 to decide to use the T-test in favor of the Z-test.
We compute the t-statistic and degree of freedom:
t ![]()
d.f = 4 – 1 = 3
When we obtained the t-statistic and the degree of freedom, it’s time to look up the critical value using t-table (Appendix B) or using Python (Appendix C). The critical value is a number represents how extreme our t-statistic should be so that we can reject the Null hypothesis. In other words, if our t-statistic is ![]() the critical value, we reject the Null hypothesis.
the critical value, we reject the Null hypothesis.
With input: ![]() = 0.1, 2-tailed test, d.f = 3; we get the critical value = 2.353. Because our t-statistic is 0.58, smaller than this critical value, we end up accepting the Null Hypothesis that the sample mean is quite similar (or says, not statistically different) to 40.
= 0.1, 2-tailed test, d.f = 3; we get the critical value = 2.353. Because our t-statistic is 0.58, smaller than this critical value, we end up accepting the Null Hypothesis that the sample mean is quite similar (or says, not statistically different) to 40.
| Test your understanding |
| |
Conclusion
This blog post gives an overview of the T-family. Essentially, T-family is used in place of the Z-family when the number of sample data points is small or when we don’t know the population variance.
One-sample T-test is a T-test that examines one set of sample data, as opposed to Paired-sample and Unpaired-sample T-tests, while there are 2 sets of samples in execution. One-sample T-test is introduced in this blog post, on the other hand, the remaining 2 are in the subsequent post on the T-family.
References:
- Wikipedia’s page about Student t-test: link
- The T-table from Stanford University: link
- Scipy.stats: link
Appendix A: Degree of freedom
Degree of freedom is the number of parameters that can vary but the proposed properties can still hold. For example, we have a set of 5 numbers (from ![]() to
to ![]() ) with known mean equals 10. We can change the value of 4 numbers in these 5 to any values we want, then the property of mean equals 10 can still hold if we set the fifth-number to be equal
) with known mean equals 10. We can change the value of 4 numbers in these 5 to any values we want, then the property of mean equals 10 can still hold if we set the fifth-number to be equal ![]() (sum of the other 4 numbers). If we vary the value of all 5 numbers, the property of mean equals 10 might not hold. Thus, the degree of freedom in this example is 4.
(sum of the other 4 numbers). If we vary the value of all 5 numbers, the property of mean equals 10 might not hold. Thus, the degree of freedom in this example is 4.
Formula to get the degree of freedom of a set of n samples (and we DO know the mean of this set) is:
d.f = n – 1
Appendix B: Testing hypotheses with T-table
Reading the T-table may be a little bit different from the Z-table.
For the Z-table, we use our z-score to find the corresponding percentile (p-value) on the table. If this percentile is smaller than the significance level (![]() ), we reject the Null Hypothesis. However, with the T-table, we use the degree of freedom and the significance level to get the critical value. If our t-statistic is larger than this critical value, then we reject the Null Hypothesis. If our t-statistic is smaller than this critical value, we failed to reject the Null Hypothesis.
), we reject the Null Hypothesis. However, with the T-table, we use the degree of freedom and the significance level to get the critical value. If our t-statistic is larger than this critical value, then we reject the Null Hypothesis. If our t-statistic is smaller than this critical value, we failed to reject the Null Hypothesis.
This is a T-table:
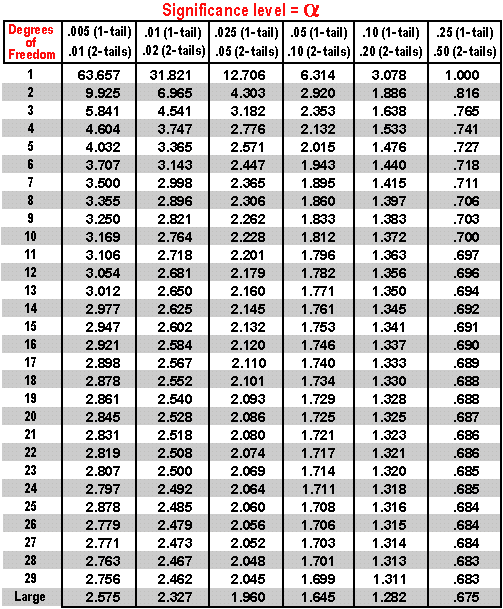
For example, we want to make a one-sided T-test with the significance level ![]() = 0.05 and have the computed t-statistic = 2.6 and degree of freedom = 20. Lookup the T-table on this d.f and
= 0.05 and have the computed t-statistic = 2.6 and degree of freedom = 20. Lookup the T-table on this d.f and ![]() , we see the critical value of 1.725, which is smaller than our real t-statistic 2.6. Hence, we conclude that we reject the Null Hypothesis and accept the Alternative Hypothesis.
, we see the critical value of 1.725, which is smaller than our real t-statistic 2.6. Hence, we conclude that we reject the Null Hypothesis and accept the Alternative Hypothesis.
Appendix C: Testing hypotheses with Python
Python’s Scipy library supports a function to query the critical value, which works just like we look up in the T-table. We should input 2 values: one minus ![]() and the degree of freedom, then the function will output the critical value.
and the degree of freedom, then the function will output the critical value.
For example, if our ![]() = 0.05, an 1-tailed test, with d.f = 20, then we call:
= 0.05, an 1-tailed test, with d.f = 20, then we call:
from scipy import stats print(stats.t.ppf(1-0.05, 20))
| 1.7247182429207857 |
With the same example, if we use a 2-tailed test, the call would be:
from scipy import stats print(stats.t.ppf(1-0.05/2, 20))
| 2.0859634472658364 |