Confidence Intervals for Linear Regression Coefficients

Test your knowledge

Confidence Intervals for Coefficients - Quiz 1

1 / 2

Regarding Linear regression, which of the below might indicate a bad feature?

The 90% Confidence Interval of that feature does not contain 0.

The 90% Confidence Interval of that feature is far from 0 and is in the negative side.

The 90% Confidence Interval of that feature is far from 0.

The 90% Confidence Interval of that feature contains 0.

2 / 2

Regarding Linear regression, suppose the assumption of error rate's normal distribution does not hold, are the Confidence Intervals reliable?

Yes.

No.

Your score is

Please rate this quiz

Confidence Interval of Coefficients?

Not only does Linear regression give us a model for prediction, but it also tells us about how accurate the model is, by the means of Confidence Intervals.

If you are not familiar with the term Confidence Intervals, there is an introduction here: Confidence Level and Confidence Interval.

For simplicity, let’s consider a simple linear regression (SLR): $\overline{y} = w_0 + w_1x_1$ . As $w_0$ and $w_1$ are estimated, we are not 100% sure if these $w_0$ and $w_1$ are really the best parameters for this problem. The actual best-parameters might be some other values, and the Confidence Interval tells us how close our parameters (i.e. $w_0$ and $w_1$ ) are to these true, best parameters.

For example, suppose our computation gives a regression line $\overline{y} = 3.5 + 8.4x_1$ , while the truth, rightful regression for the population is $y = 3.4 + 8.6x_1$ . The differences of 0.1 in $w_0$ and 0.2 in $w_1$ are the coefficients’ errors. These errors exist because the way we derive our regression is not perfectly suitable, we did not do the work well enough.

To solve this problem, Linear Regression allows us to compute the Confidence Intervals, which tells the range of regressor coefficients at some Confidence Levels.

Note that, the resulting Confidence Intervals will not be reliable if the Assumptions of Linear regression are not met. Hence, before calculating the Intervals, we should test the above assumptions to ensure none of them is violated.

How to compute the Confidence Interval of the Slope?

In this blog post, we are going to find the confidence interval of the slope ( $w_1$ ).

In Hypothesis Testing, the Confidence Interval is computed as:

CI = Mean value $\pm$ (t-statistic or z-statistic)*std

where:

t-statistic (or z-statistic) is deduced from the Confidence Level (e.g. the Confidence Level of 95% yields a Z-statistic of around 2).
std is the standard deviation of the value to be measured.

The formula is exactly the same for Confidence Intervals of Regressor Coefficients. We use t-statistic instead of z- because what we have in hand is sample data instead of the whole population. Thus, the Confidence Interval of the slope is:

CI = $w_1 \pm$ t-statistic*std $_{w_1}$

where:

the value of t-statistic depends on the Confidence Level, and we use the degree of freedom = n – 2 instead of the classical n – 1, because our regressor has 2 coefficients ( 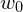$w_0$ and $w_1$ ).
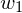std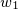: the formula for this value is a little bit involved. Ocram on StackExchange gave a full explanation here using Matrix computation. In simple words, you can think of the factors that can make the standard deviation of 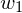increase or decrease:
- The prediction errors (or residuals) should have a direct effect on std 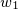$_{w_1}$ , because the higher the errors, the more erroneous our regressor is, hence the wider the Confidence Interval.
- The standard deviation of 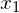$x_1$ should have an inverse effect on std 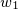$_{w_1}$ because the more diverse 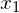$x_1$ is, the more information 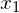$x_1$ gives, hence the more accurate of our regressor.
- The sample size (n) should have an inverse effect on std 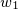$_{w_1}$ , because the bigger the sample set, the better it represents the whole population, hence the more accuracy of our regressor.

In short,

std $_{w_1}$ = $\frac{a}{b}$

where:

a = $\sqrt{\sum_{1 \leq i \leq n} (y_i - \overline{y}_i)^2}$
b = $\sqrt{(n-2) \sum_{1 \leq i \leq n}(x_{1_i} - E(x_1))^2$

Why do we compute the Confidence Intervals?

To test if each coefficient is accurate or is prone to error. For example, if the 95% Confidence Interval of a coefficient is very small, this coefficient seems to be calculated pretty well and the coefficient’s estimated value can represent its truth value.
To check whether the predictor variable does have some relation with the response variable or not. If, for example, the 90% Confidence Interval of a coefficient contains 0, maybe this predictor variable does not really have anything to do with the response variable.

Conclusion

This blog post gives an introduction to the Confidence Intervals of Linear Regression Coefficients. The Confidence Intervals help us test if the predictor variable is valuable and if it is well utilized or not.

Note that we should make sure the assumptions of Linear Regression are held before computing the CIs, as violating some of those might make our CIs inaccurate.

You can find the full series of blogs on Linear regression here.

References:

Gatech University’s lecture on LR Confidence Intervals: link
StackExchange, a question on std of coefficients: link
StatTrek’s article about CI of Regression Slope: link
Econometrics-with-r, section 5.2: link
NCSS’s book, chapter 856: link

Tung M Phung's Blog

Confidence Intervals for Linear Regression Coefficients

Leave a ReplyCancel reply