A survey of correlation analysis methods

Measuring the dependency between variables is always a crucial part in exploratory data analysis and data mining. In this article, we enumerate and give a brief summary of the popular methods for this purpose.

In general, there are 3 types of data dependency: between categorical variables, between continuous variables, and between a mix of categorical and continuous variables. Each of these types will be examined in one section below.

Dependency between categorical variables

Chi-squared

Originally, the Chi-squared (or $\chi^2$ ) is used as a statistical test. The Null hypothesis assumes that the 2 variables are independent while the Alternative hypothesis states that they are not. A highly dependent pair of variables will drive the $\chi^2$ value to a big number. The bigger the $\chi^2$ value, the less the likelihood of the data given the Null hypothesis is true, and we can take it as a sign of greater inter-dependency.

The $\chi^2$ is often computed using the contingency table. That is, given 2 categorical variables X and Y that have $k_1$ and $k_2$ different categories, respectively. The contingency table is a table T of size $(k_1+1) \times (k_2+1)$ where $T_{i,j}$ stores the number of instances that have category $i$ for X and $j$ for Y. Additionally, the (k+1)-th row and (k+1)-th column store the total value of each column and row.

Table 1 shows an example of a contingency table.

X\Y	a	b	c	total
d	120	280	200	600
e	50	250	100	400
total	170	530	300	1000

Table 1: An exemplar contingency table of 2 categorical variables X and Y.

If the 2 variables are independent, we should expect the values in any row to be proportional to the values in the last row. Similarly, the values in any column should be proportional to that of the last column.

To assess how the 2 variables are dependent on each other, we essentially compute the difference between our real data and the expectation. That is:

$\begin{aligned} \chi^2 = \sum_{i=1}^{k_1} \sum_{j=1}^{k_2} \frac{(T_{i,j} - D_{i,j})^2}{D_{i,j}} \end{aligned}$

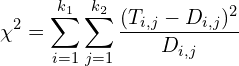
where $D_{i,j}$ is the expected number for cell $\{i,j\}$ of the contingency table, that is $D_{i,j} = \frac{T_{k_1+1,j} \times T_{i,k_2+1}}{T_{k_1+1,k_2+1}}$ .

Cramer’s V

While the $\chi^2$ value tells us a rough estimation of the dependency intensity, it doesn’t have the properties that a universal correlation coefficient should have. First, it is not bounded. The $\chi^2$ value might range from 0 to $\infty$ , while we would normally expect a maximum of 1 for perfect dependency. Second, it is not really advisable to compare the dependency intensity of different pairs of variables based on their $\chi^2$ values because this value is relative to the number of possible categories each variable has.

The Cramer’s V statistics is derived to address these weaknesses. Basically, it normalizes the $\chi^2$ value using the number of possible categories, so that the result lies in the range from 0 to 1.

$\begin{aligned}V = \sqrt{\frac{\chi^2/n}{\min(k_1, k_2)-1}}\end{aligned}$

where n is the number of data points.

Since this normalized value has taken into account the number of categories (or bins) of the participant variables, comparisons of dependencies between different pairs are now more reliable.

Mutual Information

Borrowing from the field of Information Theory, the Entropy is a measure of uncertainty in the data. The larger the entropy, the more uncertainty we are when we have to make some guess about a random instance drawn from that dataset.

Mutual Information is a natural way to estimate the shared information between 2 datasets (or in our case, 2 variables). In other words, the mutual information of X and Y is the amount of certainty we have about X if we already know everything about Y or vice versa. Another way to express it is the difference in the amount of uncertainty we have about X if we know and if we don’t know Y (and vice versa).

$I(X, Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)$

where $I(X, Y)$ is the mutual information of X and Y, $H(X)$ is the entropy of X, and $H(X|Y)$ is the conditional entropy of X given Y.

Another formula to compute mutual information from scratch is:

$\begin{aligned}I(X, Y) = \sum_{x \in X} \sum_{y \in Y} p(x, y) \log \frac{p(x, y)}{p(x) \times p(y)}\end{aligned}$

Since the value of mutual information is, similar to $\chi^2$ , in the range from 0 to $\infty$ , it is also more convenient to have it normalized, as below:

$\begin{aligned}NMI(X, Y) = \frac{2 \times I(X, Y)}{H(X) + H(Y)}\end{aligned}$

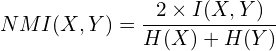
With this, we obtain a value in the decent range of [0, 1].

Thiel’s U correlation

It can be seen that the mutual information and most other dependency measurements are symmetric, i.e. how much A depends on B is equal to the amount B depends on A. In many cases, this symmetricity is desirable. However, for some other cases, especially when involving categorical variables, we may want something different. For example, looking at the 2 variables X and Y as below:

X	a	b	c	a	b	c
Y	u	v	u	u	v	u

Table 2: An example of 2 variables X and Y.

While we can infer the exact value of Y given X, the reverse does not hold. Thus, in this situation, it is more relevant if we can measure the dependency separately for each direction.

The Thiel’s U correlation supports exactly this. By mildly modifying the normalized mutual information, we have the conditional measure:

$\begin{aligned}U(X|Y) = \frac{I(X, Y)}{H(X)}\end{aligned}$

where $I(X, Y)$ is the mutual information of X and Y, $H(X)$ is the entropy of X, and U(X|Y) is the Thiel’s U dependency of X on Y. The Thiel’s U, in its pure definition, is the proportion of our uncertainty about X that can be removed if we already know Y.

For this specific example, while U(Y|X) is exactly 1 (i.e. perfect dependency), U(X|Y) is much smaller, meaning we cannot confidently predict X given the value of Y.

Dependency between continuous variables

Pearson correlation

The Pearson correlation is probably the most popular coefficient for estimating dependencies between a pair of continuous variables. It evaluates how the covariance (i.e. the joint variability of 2 variables) is compared to the product of 2 standard deviations. That is:

$\begin{aligned} \rho_{\text{Pearson}}{X, Y} = \frac{cov(X, Y)}{\sigma_X \sigma_Y} \end{aligned}$

where $\rho_\text{Pearson}{X, Y}$ is the Pearson correlation of X and Y, $\sigma$ is the standard deviation, $cov$ is the covariance, and:

$\begin{aligned} &\sigma^2_X = E[(X - E[X])^2] \\&cov(X, Y) = E[(X-E[X])(Y-E[Y])]\end{aligned}$

Intuitively, the Pearson correlation (or more specifically, the covariance, based on which the Pearson correlation is computed) measures how similar the 2 variables change with regards to their central (mean) values. Also because of this, the Pearson correlation can only detect linear relationships but not anything beyond.

One advantage of this measure is that it produces a pretty output score: a value between -1 and 1, with -1 means absolute negative association, 0 means (linearly) independent, and 1 means absolute positive association. The Pearson correlation is also easy to compute. Furthermore, since linear dependency is arguably the most common association between events in real life, sometimes, it is not necessary to consider other more complex types of relation.

Spearman correlation

In contrast to the Pearson correlation which makes use of the absolute differences between values and their mean, the Spearman correlation only considers relative differences, i.e. the differences in the rank of those values. They are intrinsically related by:

$\begin{aligned} \rho_\text{Spearman}(X, Y) = \rho_\text{Pearson}(rk(X), rk(Y)) \end{aligned}$

where $\rho_\text{Spearman}$ is the Spearman correlation, $rk(X)$ is the rank over the values of X.

Since the rank transformation is nonlinear, the Spearman can capture some types of not linear relationships (e.g. $Y = X^2$ ) but with the trade-off of precision when absolute differences actually make sense.

The Spearman correlation is often used for ordinal variables, where the ranking of values is known but their absolute distances are not (e.g. it is not clear how to quantify the differences between “very good” and “good”, and between “good” and “average”). From another point of view, the Spearman can also be used in companion with the Pearson, since $\rho_{Spearman} > \rho_{Pearson}$ might indicate a non-linear relationship in the data.

Kendall rank correlation

Another rank-based association measurement is the Kendall correlation. Similar to Spearman, the absolute values of the variables are not important for the Kendall, only their ranks matter.

To quantify the dependency between 2 continuous variables, the Kendall method examines the number of “concordant pairs” and “discordant pairs” in the data. An illustration of concordant and discordant is shown in Figure 1.

A naive count of concordant and discordant pairs requires a loop over all data points and another nested loop over all other data points, i.e. looping over all data pairs, which takes quadratic time. A more efficient algorithm was proposed by Knight [6] to compute the same numbers in $O(N \log N)$ .

The Kendall coefficient (also called Kendall tau coefficient) is then:

$\begin{aligned} \tau = \frac{\text{\#concordant pairs} - \text{\#discordant pairs}}{\binom{n}{2}}\end{aligned}$

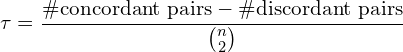
or more formally:

$\begin{aligned}\tau = \frac{2}{n(n-1)} \sum_{i<j} sgn(x_i - x_j) sgn(y_i - y_j)\end{aligned}$

The value of Kendall tau is bounded in the range from -1 to 1, with 0 means no dependency, while -1 and 1 mean perfect negative and positive relationships, respectively.

There are many arguments about comparisons between the Spearman and Kendall correlations. Most agree that the Kendall is more robust against outliers and better captures non-linear relationships, while the Spearman is preferred in the reverse case (i.e. linear dependency and fewer outliers). In practice, the Spearman correlation is more popular.

(Continuous) Mutual Information

While the Entropy is more often used on discrete variables, the same idea can be applied to continuous variables:

$h[f] = -\int f(x) \log f(x)$

where $h[f]$ is the entropy of a variable with probability density function $f$ .

When entropy can be computed, it is straightforward to apply the aforementioned dependency measures (mutual information, Thiel’s U) to the variables as if they are categorical. The problem, however, is how to get the probability density function (or pdf for short) of the continuous variables given that the data we have at hand is finite.

The simplest solution is to apply Kernel density estimation. That is, we smooth each data point into a pdf, and then sum up all of those at each position of interest to get the “mass” at that position. While the idea is plain, this method suffers from the issue of relying on human heuristics. We have to assume the shape of the distribution (usually Gaussian) and the spreading parameters (e.g. variance) ourselves.

Dcor (Distance correlation)

The distance correlation is motivated by the Pearson correlation but moves a step forward. While with Pearson, only the differences between the values and their mean are taken into account, the distance correlation considers all differences between any pairs of values. As a result, a lot more types of relationships can be captured, making this correlation coefficient more capable in general.

Given 2 variables X and Y, we first compute the distance matrices $a_{j,k}$ and $b_{j,k}$ independently for each variable:

$a_{j,k} = || X_j - X_k ||$ ,

$b_{j,k} = || Y_j - Y_k ||$ ,

where || . || is the Euclidean distance. Note that for distance correlation, the value type of a variable may be either a scalar or a vector of values. If it is a scalar, the Euclidean distance is nothing more than the absolute operator.

Then, the doubly centered distance matrices A and B are formed by:

$A_{j,k} = a_{j,k} - \bar{a}_{j.} - \bar{a}_{.k} + \bar{a}_{..}$

$B_{j,k} = b_{j,k} - \bar{b}_{j.} - \bar{b}_{.k} + \bar{b}_{..}$

where $\bar{a}_{j.}$ denotes the mean of $a$ ‘s j-th row, $\bar{a}_{.k}$ denotes the mean of $a$ ‘s k-th column, and $\bar{a}_{..}$ the mean of the whole matrix $a$ .

The idea behind this doubly centered transformation is to move the centers of all rows and all columns to the origin. That is, the sum of each row (or each column, or the whole matrix) is 0 for both $A$ and $B$ . With this, each point can then be thought of as a vector from the origin, and their distances, or similarities, can be computed using the dot product.

The squared distance covariance is then:

$\text{dCov}^2(X, Y) = E[A_{j,k}B_{j,k}]$

or equivalently, we can just flatten A and B and compute their covariance:

$\text{dCov}^2(X, Y) = cov(\text{flatten}(A), \text{flatten}(B))$

The distance correlation equals to the distance covariance divided by the product of individual standard deviation (this formula is entirely inherited from regular Pearson correlation and covariance):

$\begin{aligned} \text{dCor}(X, Y) = \frac{\text{dCov}(X, Y)}{\sqrt{\text{dVar}(X)\text{dVar}(Y)}} \end{aligned}$

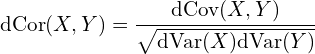
The advantage of distance correlation in comparison to the Pearson correlation is obvious since it can capture non-linear relationships between variables. There are, however, some downsides to that. First, since distance correlation is a non-parametric method, it usually requires a lot more data to work well. Second, the output score it returns is a scalar in the range from 0 to 1 (with 0 means independence and 1 means maximal association), which means there is no sign (positive or negative) of the relationship. Last, the time complexity is quadratic, while it is linear for the Pearson correlation.

MAC (Multivariate Maximal Correlation Analysis)

This is a method to estimate the total correlation of 2 or more continuous variables. This method follows the class of maximal correlation analysis. That is, it tries many possible ways to split the continuous values into bins and calculate (and return) the maximum correlation among those ways. For each binning realization, the correlation is represented by the mutual information. Roughly speaking, the mutual information is:

$\begin{aligned} I(D) = \sum_{i=1}^d H(X_i) - H(X_1, X_2, ..., X_d) \end{aligned}$

where D is the dataset, d is the number of variables, H is the entropy function, and $X_i$ is the i-th variable.

This idea was previously studied by Reshef et al [1] (that method is called MIC). The novel contributions of MAC involve:

its ability to work with more than 2 variables,
the use of cumulative entropy as a substitute for regular entropy,
the elimination of heuristic optimizations.

Overall, it can be seen that MAC outperforms its older brother (MIC) and Dcor in many scenarios, including when there are multiple levels of noise in data.

For detailed explanation, please refer to the original paper by Nguyen et al.

Dependency between categorical and continuous variables

2-sample T-test

If we want to infer the dependency between a binary variable and a continuous variable, the 2-sample T-test is a common choice. In particular, we can use the independent 2-sample T-test, which is originally targeted for testing the hypothesis of whether the means of the 2 groups are different. As we have a binary variable, the data can be split into 2 groups according to its binary values.

Since this T-test has been discussed in another post, we are not going into the details here. Nevertheless, it is worth it to mention the underlying assumptions of any T-test:

Each data point is generated independently and identically.
The data in each group should be approximately normally distributed.
No or small effects from outlier.
The groups should have the same variance, especially if the sizes are vastly different. If this assumption is violated (but other assumptions still hold), it is advised to use Welch’s t-test, a modification that allows different variances among groups.

Either the T-statistic or the p-value can be used as a measure for dependency. The larger the absolute T-statistic (or the smaller the p-value), the more the 2 variables are dependent to each other.

ANOVA

If we have a multi-categorical variable and a continuous variable then the One-way ANOVA is a good candidate. Similar to the T-test, the One-way ANOVA is also a hypothesis testing method for whether the groups are different. We can also call this a F-test because its outcomes follow a F-distribution.

We treat each possible value of the categorical variable as a group, then the values of the continuous variable are distributed to their corresponding groups. Next, we essentially compare the variance between groups and the variance within groups to see if the groups are likely generated from the same distribution or not. If the variance between groups is much higher than the variance within groups, we conclude that those groups are different, and thus the categorical variable (which splits data into groups) really have some association with the continuous variable. In the reverse case, we see no different between the groups, inferring that the 2 variables are more independent.

While the idea is quite simple, it requires quite a few computations to get the F-statistic of this test. For brevity of the article, we refer readers to this wiki page for detailed formulas and examples.

Note, however, that the One-way ANOVA has the same assumptions as of the 2-sample T-test: iid, normal distribution, equal variance, and no outliers. If the assumption about equal variance is the only one that does not hold, we should use Welch’s t-test (we mentioned this one above), a variant of the T-test which not only takes into account the difference in variances but also can be generalized to more than 2 groups.

Similar to the One-way ANOVA that examines how one categorical variable affects the continuous variable, we have Two-way, Three-way, or n-way ANOVA that work the same for 2, 3, or n categorical variables and one continuous variable. The One-way and Two-way are most common, while the others are rarely used due to the difficulty of interpreting their result.

References:

[1] Detecting Novel Associations in Large Data Sets, Resher et al., 2011, pdf
[2] Measuring and testing dependence by correlation of distance, Székely et al., 2007, pdf
[3] Multivariate maximal correlation analysis, Nguyen et al., 2014, pdf
[4] Distance correlation, wiki
[5] Intuition about distance correlation, ttnphns, a StackExchange answer
[6] A Computer Method for Calculating Kendall’s Tau with Ungrouped Data, Knight, 1966, pdf
[7] One-way Analysis of Variance, wiki
[8] Welch’s t-test, wiki

2 thoughts on “A survey of correlation analysis methods”

Sharif Ahmed says:

September 2, 2022 at 7:11 pm

Hello, very interested articles. I am doing a PhD and how can we connect? I am doing a correlation analysis but not sure which approach will be good.

1. Tung.M.Phung says:
  
  September 12, 2022 at 3:50 pm
  
  Hi Sharif,
  Sorry for my late reply.
  Please feel free to drop me a message and friend request on LinkedIn. I’m really happy to connect.
  
  Cheers,
  Tung

Tung M Phung's Blog