
| Test your knowledge |
| |
What is a Paired 2-sample T-test?
Let’s analyze this definition from scratch.
Thus, in summary, a Paired 2-sample T-test takes as input 2 sample sets that have their observations linked to the other on a 1-to-1 basis, and the test’s outputs follow a T-distribution. This is also abbreviated as the Paired T-test or Dependent T-test.
In contrast to the Paired 2-sample T-test, we also have the Unpaired 2-sample T-test.
| Paired 2-sample T-test | Unpaired 2-sample T-test | |
| Usage | When each observation in a sample set is semantically related to one and only one observation in the other set. | When the requirement of correspondence for the Paired 2-sample T-test does not hold. |
| Usecase examples | We have a soft-skill course. We measure the performance of our company’s employees before and after learning the course to see if this course enhances employee productivity. We do A/B Testing on our ads. For each of our webpages, blue-colored theme ads are shown for some guests while yellow-colored theme ads are shown to the others. After a day, we have 2 sets of sample data, one contains the average click-through rate (for ads) of each webpage when blue ads are shown, the other contains the same measure for yellow ads. We compare these 2 sets to see if one color is significantly more attractive than the other. | There are 2 sample sets, one is the weights of 30 men and the other is the weights of 30 women. We want to test if the weight is significantly different for different genders. We do A/B Testing on our ads. For some random webpages, we show ads with blue-colored themes, while for the other webpages, yellow-colored theme ads are shown. After a day, we have 2 sets of sample data, one contains the average click-through rate (for ads) of each webpage that is attached with blue ads, the other contains the same measure for webpages with yellow ads. We compare these 2 sets to see if one color is significantly more attractive than the other. |
| Sample sizes | The sizes of the 2 sample sets must be the same. | 2 sample sets may have different sizes. |
Notice that the result taken from the Paired Test is more significant than from the Unpaired Test given the same samples (because the 1-to-1 relationship gives additional information), it is recommended to take the Paired Test if possible (i.e. if the conditions for a Paired Test hold).
Assumptions
The Paired 2-sample T-test is a parametric test, thus it requires some assumptions to be true (or at least approximately true):
Note that even though the tests’ general goal is to check if the means of the 2 distributions are equal or not, it is usually the case that it checks whether the 2 distributions are the same or not. That is, we usually assume the variances of the 2 distribution are equal, then we test if the means are also equal (both the means and variances are equal indicates that the 2 distributions are also the same) or not (implies that 2 distributions are not the same).
Conduct the Test
The Paired 2-sample T-test is just a One-sample T-test in disguise. Put it another way, we can transform the Paired T-test into a One-sample T-test.
This transformation can be elaborated by restating the problem: we want to test if the 2 sample sets are generated by the same distribution, which is identical to test if the differences between them are generated by a distribution with mean 0.
Call:
- n as the size of each sample set.
 and
and 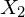 as the 2 sets, where the i-th observation of
as the 2 sets, where the i-th observation of  (
(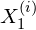 ) is related to the i-th observation of
) is related to the i-th observation of 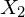 (
( ),
),  .
. as the set of differences between each observation in
as the set of differences between each observation in  with the correspondence in
with the correspondence in 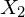 . (
. ( .)
.)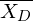 is the mean of
is the mean of  .
. is the sample standard deviation of
is the sample standard deviation of  . Note that this is the sample std, so we compute the unbiased std (i.e. divide by n-1 instead of n).
. Note that this is the sample std, so we compute the unbiased std (i.e. divide by n-1 instead of n).
Here, the T-statistic is taken by:

with the degree of freedom DF = n – 1.
After getting the T-statistics and the degree of freedom, we can verify our hypothesis using the T-table (or with the help of Python, or other means) as previously described here.
Example
Suppose we want to measure the effectiveness of a diet. We gauss the weights of 10 people before and after practicing the diet to verify if there is any statistical difference. The weights are shown in the table below, where each row represents 1 person.
| Weight before diet ( | Weight after diet ( |
| 50 | 52 |
| 74 | 70 |
| 65 | 58 |
| 80 | 79 |
| 66 | 66 |
| 58 | 53 |
| 49 | 47 |
| 54 | 55 |
| 71 | 60 |
| 55 | 52 |
Let’s suppose our significance level (![]() ) is 0.05.
) is 0.05.
To solve this problem, firstly, we make the set of differences, ![]() .
.

Secondly, we calculate the mean and standard deviation of this set:
![]()
![]()
The T-statistic is then:
![]()
with the degree of freedom DF = n – 1 = 9.
Look up the T-table, we take it that the Critical Value for ![]() of a 2-tailed test with DF = 9 is 2.262, which is smaller than our T-statistic 2.405. Hence, we conclude that the impact of the diet is statistically significant.
of a 2-tailed test with DF = 9 is 2.262, which is smaller than our T-statistic 2.405. Hence, we conclude that the impact of the diet is statistically significant.
| Test your understanding |
| |
References: