
| Test your knowledge |
| |
Anything which has advantages should also have disadvantages (or else it would dominate the world). Below, I will talk about the drawbacks of Linear regression. If you are considering using LR for your production pipeline, I would recommend taking a careful read of this blog, along with the Assumptions of Linear regression.
The 4 disadvantages of Linear regression are:
Linearity-limitation
Linear regression, as per its name, can only work on the linear relationships between predictors and responses.
Although we can hand-craft non-linear features and feed them to our model, it would be time-consuming and definitely deficient. Linear regression lacks the built-in ability for capturing non-linearity association. Hence, if you want to mine or derive some non-linear relationship in your data, LR is probably not your best choice.
Moderate performance (usually)
As its assumptions are too strong, Linear regression can rarely demonstrate its full power, which leads to inferior predictive performance over its peers.
The first assumption, which is not only arguably the most crucial, but also the one almost always gets violated is the requirement about linearity. Real-world problems are generally more complicated than Linear regression perceives, thus the cause for under-fitting.
However, even being infrequent, there are still cases where Linear regression can show its strength. An example is the House Price Prediction Competition on Kaggle.
Uncertainty in Feature importance
While the weight of each feature somehow represents how and how much the feature interacts with the response, we are not so sure about that. The weight does not only depend on the association between an independent variable and the dependent variable, but also the connection with other independent variables.
For example, in cases of high multicollinearity, 2 features that have high correlation will “steal” each other’s weight. If you run stochastic linear regression multiple times, each time these 2 features can have different weights. So it’s really hard for us to determine their significance.
Fear of outliers
Linear regression, or particularly OLS – the most common model in the family of Linear regression, is very sensitive to outliers.
If the outliers in data are just extreme cases, and still follow the trends of normal data points, it would be fine. But if those outliers are, in fact, noise, they will cause huge damage.
Imagine you use MSE as your objective function, a bigger error will cause a much higher impact than a smaller one. A mere outlier, in this case, can pull the regression line toward itself by quite an angle. Let’s look at the below graph and you will see it.
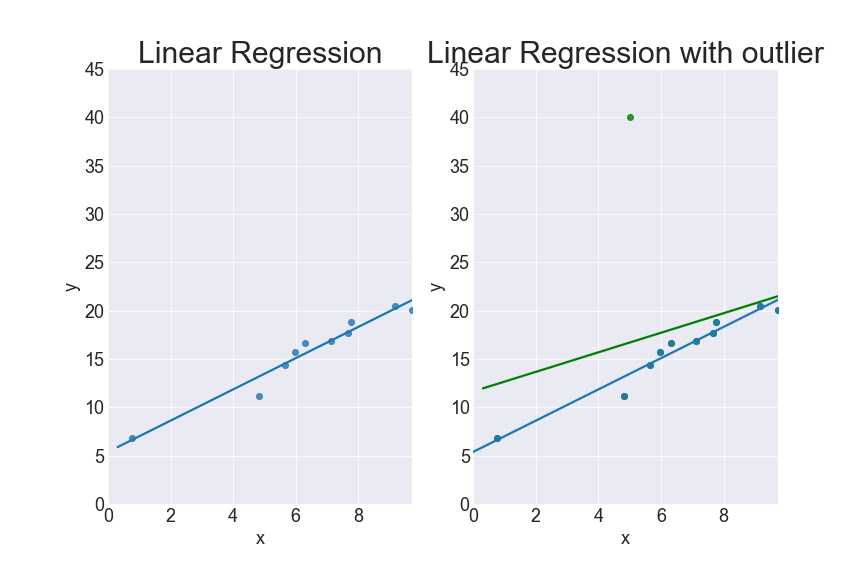
On the right: the green line is the linear regression when there is an outlier in the data, compared to the blue line – linear regression with no outlier.
There is some research on this problem, which is called Robust Regression.
You can find the full series of blogs on Linear regression here.